프로그래밍 관련 정보

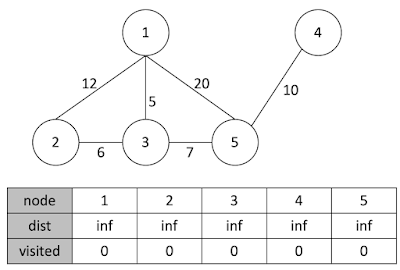
다익스트라 알고리즘 Overview 그래프 최단 경로를 찾는 알고리즘으로서, 특정한 하나의 정점 노드에서 다른 모든 정점 노드로 가는 최단 경로를 구하는 알고리즘입니다. ( 시간복잡도: $O(V^{2}$) ) 다익스트라 알고리즘은 그리디와 동적 프로그래밍 알고리즘 모두로 보고 있습니다.  왜 둘다로 여기는지는 참고 사이트 와 아래 Introduce를 확인해주세요. * 다익스트라 알고리즘은 음의 간선이 존재하지 않는 경우 사용할 수 있습니다. Introduce 카카오나 네이버 맵 등에서 출발지부터 도착지까지 가장 빠른 경로를 어떻게 찾아서 알려줄까요? 이럴 때 다익스트라 알고리즘을 사용합니다. 다익스트라 알고리즘은 컴퓨터 과학자인 Edsger W.Dijkstra로부터 1956년에 만들어진 그래프에서 단일 최단 경로를 찾는 알고리즘입니다. 이는 특정 정점으로부터 연결된 모든 정점의 최단 경로를 찾는 알고리즘이란 뜻입니다. 이 과정에서 도착 정점 뿐만 아니라 다른 모든 정점의 최단 경로까지 찾습니다.  즉, 매번 최단 경로의 정점을 선택해 탐색 반복하며(그리디 알고리즘 성격), 정점과 정점 사이 경로 갱신을 위해 이전에 구했던 경로 값을 사용합니다. (다이나믹 알고리즘 성격)  다익스트라 알고리즘은 유방향(directed)과 무방향(undirected)에서 양의 간선인 경우 동작 가능합니다. 유방향 (directed): 방향이 있는 간선을 가지는 그래프 (간선은 단방향 관계를 나타냄) 무방향 (undirected): 방향이 없는 간선을 가지는 그래프 (간선은 양방향 관계를 나타냄) Algorithm 1. 출발 정점 설정 (출발 정점 최소 비용은 0으로 설정, 자기자신으로 이동하는 비용이기 때문) 2. 정점 방문 여부를 체크하는 리스트 생성 (visited list) 3. 최단 거리 리스트 생성 (dijkstra list) 4. 선택된 정점의 인접한 정점들 중, 아직 방문하지 않았고 비용이 가장 적은 정점 선택 5. 4번

Union-Find 대표적인 그래프 알고리즘으로 상호 배타적 집합(Disjoint Set)을 표현할 때 사용합니다. 상호배타집합이란? 서로 중복으로 포함된 원소가 없는 집합들을 상호배타집합 혹은 서로소 집합이라 부릅니다. A = {1, 2}, B = {3, 4} = Disjoint Set A = {1, 2}, B = {2, 3, 4} = Not Disjoint Set (2가 중복되기 때문에) 그래프 문제에서 여러 개체를 집합으로 "합치거나" 개체가 어떤 집합에 있는지 "찾을 때" 사용하기 때문에, Union-Find라고 부르며, 이 때 주어진 개체들이 중복된 값을 가지지 않으면 상호배타집합이라 부를 수 있습니다. Union-Find 알고리즘은 단독으로 사용되는 경우는 별로 없고, 다른 알고리즘을 구현하는 과정에서 많이 사용됩니다. 대표적으로 최소비용 신장트리 (MST)를 만드는 크루스칼 알고리즘에서 Union-Find를 이용합니다. 1. Union-Find 연산 Union-Find 지원 연산은 크게 Init(초기화), Union(합치기), Find(찾기) 연산으로 나뉩니다. 위와 같이 여러 개의 개체(노드)가 있다고 가정하겠습니다. Init(초기화) 개체가 어떤 집합에 속해있는지 확인하기 위한 lookup 테이블을 만듭니다. 최초 각 개체는 자기를 제외한 다른 개체들과 집합을 이루지 않기 때문에 자기 자신이 집합의 대표자가 됩니다. 대표자란 각 집합마다 1개씩 있는, Union-Find에서 집합을 구분하는 데 사용되는 원소를 의미합니다. Union (합치기) union(x, y)를 하면 x, y 원소가 속한 2개의 집합을 하나의 집합으로 합칩니다. 여기서 x, y 원소를 합치는게 아니라 x, y가 속한 "집합"을 합친다는 것에 유의해주세요. "집합"을 합치기 위해 초기화 과정에서 생성한 lookup 테이블의 "대표자"를 이용합니다.

카데인 알고리즘 DP (Dynamic Programming) 기법 중 하나로서, 각 수들을 더했을 때 가장 큰 수가 나오는 연속된 부분을 찾는 알고리즘 ( 시간복잡도: O(n) ) local_max[i] = max (A[i] + local_max[i- 1 ] , A[i]) 많은 분들이 Maximum Subarray Problem 문제 해결방법을 알아보다 카데인 알고리즘을 알게되었을텐데, Maximum Subarray Problem을 통해 카데인 알고리즘을 알아보겠습니다. Maximum Subarray Problem (최대 부분 합 구하기) 최대 부분 합 구하기 문제는 주어진 1차원 배열의 부분 배열에서 최대 합을 가지는 값을 구하는 문제입니다. A = [- 2 , 1 , - 3 , 4 , - 1 , 2 , 1 , - 5 , 4 ] 위 배열에서 가장 큰 합을 가지는 부분 배열은 [4, -1, 2, 1]이며, 최대 합은 6이 됩니다. 저를 포함하여 대다수가 Brute Force로 접근했을텐데 Brute Force를 간단하게 알아보겠습니다. Brute Force 접근 인덱스 0부터 N-1까지 모든 부분 배열의 합을 구한 뒤, 부분 배열의 합 중 가장 큰 값을 찾는 방식 A[0]부터 A[0..1], A[0..2], A[0..N-1]까지 모든 부분 합을 구한다. Sum 배열에 등록된 A[0]의 모든 부분 합 중, 가장 큰 부분 합(local_max)을 구한다. 1,2 를 반복한다. (A[1]부터 A[1..2], A[1..N-1]까지 local_max 구하고, A[2]에서 local_max 구함을 반복) 0부터 N-1까지 구한 local_max[0...N-1]에서 가장 큰 값(global_max)을 구한다. global_max를 리턴 위 방법은 배열의 사이즈가 커지는 만큼 1-2번을 반복해야하는 횟수도 커집니다. ( 시간 복잡도: O(n 2 ) ) 또한 이미 A[i]에서 구했던 값을 A[i+1]에서 다시 구해야하는 문제가 존재합