[Algorithm] Union-Find 정리
Union-Find
대표적인 그래프 알고리즘으로 상호 배타적 집합(Disjoint Set)을 표현할 때 사용합니다.
상호배타집합이란?
서로 중복으로 포함된 원소가 없는 집합들을 상호배타집합 혹은 서로소 집합이라 부릅니다.
A = {1, 2}, B = {3, 4} = Disjoint Set
A = {1, 2}, B = {2, 3, 4} = Not Disjoint Set (2가 중복되기 때문에)그래프 문제에서 여러 개체를 집합으로 "합치거나" 개체가 어떤 집합에 있는지 "찾을 때" 사용하기 때문에, Union-Find라고 부르며, 이 때 주어진 개체들이 중복된 값을 가지지 않으면 상호배타집합이라 부를 수 있습니다.Union-Find 알고리즘은 단독으로 사용되는 경우는 별로 없고, 다른 알고리즘을 구현하는 과정에서 많이 사용됩니다. 대표적으로 최소비용 신장트리 (MST)를 만드는 크루스칼 알고리즘에서 Union-Find를 이용합니다.
1. Union-Find 연산
Union-Find 지원 연산은 크게 Init(초기화), Union(합치기), Find(찾기) 연산으로 나뉩니다.
위와 같이 여러 개의 개체(노드)가 있다고 가정하겠습니다.
Init(초기화)
개체가 어떤 집합에 속해있는지 확인하기 위한 lookup 테이블을 만듭니다.
최초 각 개체는 자기를 제외한 다른 개체들과 집합을 이루지 않기 때문에 자기 자신이 집합의 대표자가 됩니다.
대표자란 각 집합마다 1개씩 있는, Union-Find에서 집합을 구분하는 데 사용되는 원소를 의미합니다.
Union (합치기)
union(x, y)를 하면 x, y 원소가 속한 2개의 집합을 하나의 집합으로 합칩니다.
여기서 x, y 원소를 합치는게 아니라 x, y가 속한 "집합"을 합친다는 것에 유의해주세요.
"집합"을 합치기 위해 초기화 과정에서 생성한 lookup 테이블의 "대표자"를 이용합니다.
만약, x, y 원소가 속한 집합의 대표자가 동일하다면 union 연산은 실행되지 않습니다.
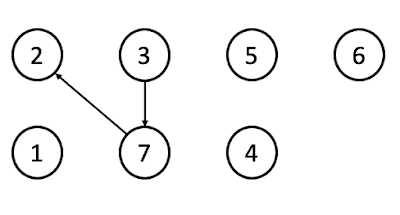
union(7, 3)일 경우 7과 3 원소가 속한 2개의 집합을 하나의 집합으로 합친다는 의미입니다.
union을 할 경우 왼쪽을 기준으로 오른쪽 집합을 합칠수도 있고, 더 작은 원소 값을 기준으로 값이 큰 원소의 집합을 합칠 수도 있습니다. 여기서는 왼쪽 원소의 집합(7)을 기준으로 오른쪽 원소의 집합(3)을 왼쪽 원소 집합으로 합치겠습니다. ( 3 원소 집합을 7 원소 집합에 포함 )
3이 7 집합으로 합쳐졌기 때문에 lookup 테이블에서 3 원소 대표자를 7로 수정합니다.추가적으로 union(2, 7)를 하게 되면 7 원소가 속한 집합이 2가 속한 원소의 집합인 2에 합쳐집니다.
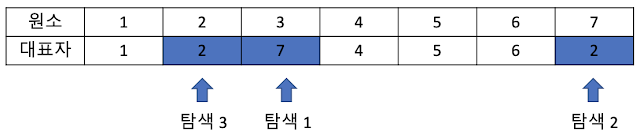
lookup 테이블에서 7 원소 대표자를 2로 수정합니다. (2와 7를 합쳤기 때문에)Find (찾기)
입력된 원소의 대표자를 찾습니다.위에 union된 집합을 기준으로 Find(3)을 하게 되면 대표자 2를 반환합니다.
2. Union-Find 최적화
편향 트리일 때 lookup 테이블 구조
편향 트리 일 때 find(5)를 하면 5 원소의 대표자 4를 찾고 4 원소의 대표자 3을 찾는 행위를 반복하면서 마지막으로 대표자 1을 찾아 값을 반환합니다.
트리를 이용하는 중요한 이유 중 하나가 빠른 탐색 속도인데 최악의 경우는 선형 탐색 속도를 가지게 됩니다.
이를 해결하기 위한 방법으로 경로 압축(Path Compression) 방법이 있습니다.
경로 압축 (Path Compression)
union(2, 7)을 하는 과정에서 7 원소의 대표자만 2로 수정을 하고 있습니다. (3 원소의 대표자는 7)
위 방식은 lookup 테이블에서 3 원소의 대표자 7를 찾은 다음 7 원소의 대표자 2를 찾는 방법으로 원소 - 대표자 탐색을 반복하기 때문에 수행 속도가 오래 걸리게 됩니다.
수행 속도를 줄이는 게 목표이기 때문에 union(2, 7)을 할 때 7 원소 대표자와 3 원소 대표자를 모두 2로 수정합니다.
Union-Find 알고리즘에서 Find는 오직 대표자를 찾기 위한 목적이기 때문에 루트 노드만 빨리 찾으면 됩니다. (중간 과정 필요 X)
트리의 좌우를 넓게 만들고 깊이를 줄이는 방식으로 Find 수행 속도를 빠르게 할 수 있습니다. (시간 복잡도: O(1))
3. Union-Find 정리
Union-Find는 Init(초기화), Union(합치기), Find(찾기) 3가지 연산으로 구분됩니다.Union 과정에서 원소의 대표자만을 갱신할 경우 Find() 연산에서 최악의 경우 O(N) 만큼의 시간이 소요됩니다.
Find()에서 수행 속도를 단축하기 위해 경로 압축이라는 방법을 이용하면 Find() 수행 속도를 빠르게 할 수 있습니다.
Union-Find는 단독으로 사용되기 보단, 다른 알고리즘을 구현하는 과정에서 많이 사용됩니다.
특히 그래프 연결성 확인에서 많이 다뤄지기 때문에 Union-Find를 적용하여 문제를 쉽게 해결할 수 있습니다.
최대한 쉽게 설명하고자 했지만 이해되지 않는 부분이나 잘못된 부분은 댓글 부탁드립니다.
감사합니다.













댓글
댓글 쓰기